來源:中國商界雜志社
這個冬天,“羽絨服”成了社交媒體平台熱搜榜上的常客,“羽絨服該怎么买”也成爲人們頻繁討論的話題。
在市場上,今年以來,高梵、skypeople(天空人)等走高端路线的新生代羽絨服品牌正快速闖入消費者的視野。隨着近期羽絨市場虛假宣傳、以次充好等負面問題的曝光,消費者對羽絨服品質的關注度有所提升,這些帶有“高端”標籤的品牌似乎因此獲得了不錯的銷售表現。這些品牌的賣點是什么,它們能輕易撼動波司登、鴨鴨、雅鹿等“老牌”羽絨服在市場中的地位嗎?
“高端”羽絨服搶佔市場
這個冬天,高梵投放的戶外廣告比往年多了不少。不管是在繁華的商業街上,還是在小區的電梯裏,身着“潮奢風”鵝絨服的新代言人楊冪的招貼隨處可見。

北京市某小區電梯內投放的高梵廣告。
資料顯示,高梵成立於2004年,創始人爲吳昆明。不過,該品牌开始更廣泛受到市場及消費者的關注,還是在2021年其轉型發力线上並推出首款“黑金鵝絨服”之後。
從品牌定位來看,高梵走的是高端產品路线。據抖音高梵官方旗艦店客服介紹,“黑金”是高梵鵝絨服的統稱,其中,“黑珍珠”系列填充了該品牌最高品質的鵝絨,今年“黑珍珠”已升級至4.0版本。

展開全文
高梵爆款產品“黑珍珠”系列鵝絨服。
在定價上,高梵大部分產品的售價在2000元至4000元之間。天貓旗艦店顯示,“黑珍珠”4.0六格鵝絨服的吊牌價爲3899元,“先鋒”3.0八格鵝絨服優惠前的價格爲2500元。
雖然定價不低,但高梵今年確實賣得很火。在高梵天貓旗艦店,“先鋒”3.0六格和八格鵝絨服都顯示“1萬+人付款”,並且24小時內購买人數超過200人。此外,根據高梵的介紹,今年11月25日新代言人楊冪亮相直播間,當場直播吸引了超過2000萬余人次觀看,品牌账號因此登頂抖音平台羽絨服账號榜。
另一個迅速成長的高端羽絨服品牌是猿輔導旗下的“skypeople天空人”。品牌官網顯示,skypeople2022年起步於中國本土,是一家“羽絨科技公司”。
天貓旗艦店顯示,skypeople羽絨服價格分布在2800元至9999元。記者在北京skp商場限時店走訪時,門店銷售人員表示,品牌线上线下全年無折扣。因爲定價高,skypeople此前在消費者中引發爭議。不過,天貓銷售頁面顯示,即使售價已達到5800元,一款男士羽絨派克服在一周內仍有超過100人購买。

skypeople北京skp商場限時店。
另據了解,skypeole在线下渠道不斷將實體店开進黃金地段。截至目前,品牌在全國共开設12家門店(包括長期門店及限時店),所在商場包括北京skp、北京三裏屯太古裏、上海來福士、杭州萬象城等。
“高端”羽絨服有何賣點
前有波司登、鴨鴨等老牌羽絨服“穩拿”大部分市場份額,新生代羽絨服品牌想要獲得消費者更廣泛的關注,自然要有獨特的賣點。
在上述skypeople男士羽絨派克服天貓旗艦店銷售頁面,有消費者發出“靈魂提問”:這衣服貴在哪裏?到底值這個錢嗎?
對此,skypeople官方的回復是:該款產品採用了WarmBox箱式充絨設計,填充800蓬松度的白鵝絨,保暖效果顯著。外層使用Pertex 3L防護面料,有效防風雨,保持溫暖。產品選用高品質材料,並經過嚴格的工藝標准生產,以確保最佳的舒適效果。
skypeople提到的充絨工藝和面料材質,正是品牌一貫強調“科技感”的體現。在宣傳頁面中,該品牌提出,充絨技術是羽絨產品的核心,skypeople全系列羽絨產品將常規的4層充絨結構改爲超輕的2層或3層結構,讓羽絨服做到“又輕又暖”。此外,科技面料的運用也讓羽絨服在防風防雨、透溼和延展性方面表現出色。

skypeople部分產品款式。
一名戶外服飾業內人士認爲,skypeople宣稱的“全系800蓬松度羽絨”對整個戶外行業來說確實不太容易做到。不少已經購买過skypeople的消費者,都對品牌和產品給出了相對積極的評價。在淘寶平台,有消費者評價稱:“一般派克服都挺重的,但這家的很輕。”一位近日在线下選購了skypeople面包服的北京消費者表示:“雖然價格不低,但這款羽絨服的西山綠色很好看、很顯白,800蓬松度和超輕的重量也讓人在冬天的安全感拉滿。”
對於高梵而言,專注“鵝絨服”是其最突出的賣點。
在抖音官方旗艦店,直播間內的主播多次強調,高梵是“唯一一家專注做鵝絨服的品牌”。在各種戶外廣告中,“高端鵝絨服銷量第一”也被品牌寫在了顯眼位置。
“我們家所有產品填充的都是鵝絨,其中‘黑珍珠’用的是‘飛天絨皇’,絨子含量95%,清潔度達到1000+,蓬松度達到800+。‘黑珍珠’系列是品牌的爆款,最近時常賣斷貨。”在高梵北京skp商場限時店,銷售人員向記者介紹。
除此之外,無論是线上還是线下,“高定”一詞都頻繁出現在高梵的宣傳語中。高梵宣稱,品牌是“全球皇室高定鵝絨服的標准制定者”,在巴黎、米蘭、上海設有三大奢研中心,品牌全球創意總監曾在國際知名高端消費品牌擔任設計師。

在高梵北京限時店內,“高定設計”“高定工藝”等賣點被突出展示。
來自東北地區的消費者孫女士告訴記者,今年入冬後,她打算新买一件羽絨服。前段時間媒體集中曝光了劣質羽絨服泛濫的問題,這讓她對羽絨服品質的關注度有所提升。對羽絨種類、參數做過一番功課後,她決定購买一件鵝絨服,並最終從一衆品牌中選擇了高梵。
“感覺高梵的填充物比較好,外觀上既簡約又耐髒,很實用。”孫女士說。
新生代品牌能站穩腳跟嗎
《2024天貓服飾羽絨市場多元場景趨勢月刊》提出,我國羽絨市場目前正呈現性價比與高端品質商品並駕齊驅的局面。在消費者群體中,選購200元至400元高性價比羽絨服的群體佔比最高,1000元以上價位段增速同樣顯著,彰顯了消費者對品質與時尚的高要求。
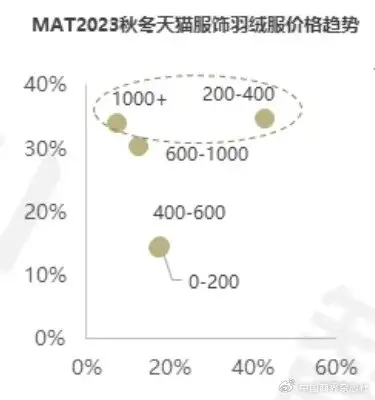
MAT2023秋冬天貓服飾羽絨服價格趨勢。(圖片截自《2024天貓服飾羽絨市場多元場景趨勢月刊》,數據來源:阿裏消費洞察)
在這一趨勢下,服裝企業近年正在越來越快地搶佔中高端羽絨服市場。2023年,貓人集團推出“美力城”服飾品牌,其羽絨服同樣以鵝絨填充和高科技面料爲賣點。同年,歌力思宣布與加拿大高端羽絨服品牌Nobis籤署合資經營協議,擬在深圳設立合資公司,負責Nobis品牌在中國內地及港澳地區的發展和運營工作。今年10月,波司登與加拿大高端外套品牌慕瑟納可(Moose Knuckles)達成战略合作協議,旨在進一步優化波司登集團品牌矩陣。
高端羽絨市場“火”了,品牌想要保持長期熱度,容易嗎?
在時尚產業獨立分析師、上海良棲品牌管理有限公司創始人程偉雄看來,這些新興品牌的未來表現仍然有待時間檢驗。
以高梵爲例,近幾年品牌經歷轉型升級後,將經營重心放到了线上渠道。北京skp限時店銷售人員表示,目前高梵僅在沈陽及北京擁有實體店。

高梵北京skp限時店外觀。
程偉雄認爲,從高梵現階段的銷售策略來看,僅依賴线上渠道似乎還顯得不夠扎實。如果沒有线下實體店支撐,品牌就難以實現從輕資產到重資產的轉變,也就難以維系其穩定性和消費者對其的信任。
“品牌從线上向线下發展,需要對相關體系進行重構,包括產品體系、研發體系、渠道體系和組織運營體系等。”程偉雄說。
高梵北京限時店銷售人員告訴記者,明年品牌或考慮开設更多线下門店。
標題:今年的羽絨服,流行走高端路线了?
聲明: 本文版權屬原作者。轉載內容僅供資訊傳遞,不涉及任何投資建議。如有侵權,請立即告知,我們將儘速處理。感謝您的理解。
