記者潘慧中/綜合報導
林襄、林穎樂18日被黃小柔具名直指出外景佔位後,掀起社會譁然。沒想到,徐凱希20日凌晨發文「我真的好佩服說謊被拆穿還能完全不承認的人,到底哪來的勇氣」後,居然被網友懷疑在影射林襄、林穎樂。對此,她稍早親上火線反駁了!
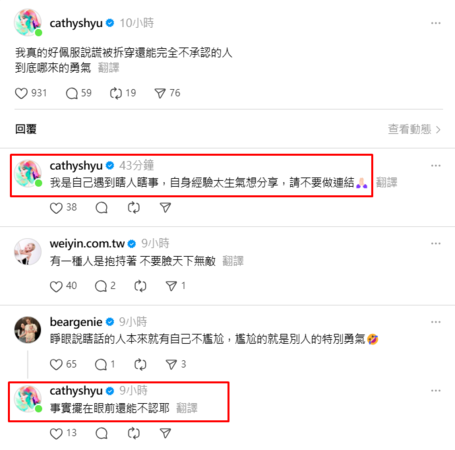
徐凱希20日凌晨在Threads抒發個人情緒後,接連釣出鮪魚(徐瑋吟)、熊熊(卓毓彤)回應。鮪魚直言「有一種人是抱持著不要臉天下無敵」,熊熊也不客氣地說:「睜眼說瞎話的人本來就有自己不尷尬,尷尬的就是別人的特別勇氣。」

但萬萬沒想到,這則貼文讓不少網友懷疑徐凱希是否在影射林襄、林穎樂。對此,徐凱希稍早在留言區澄清,真的沒有在影射林襄、林穎樂,「我完全沒在討論那件事,請別腦補。」
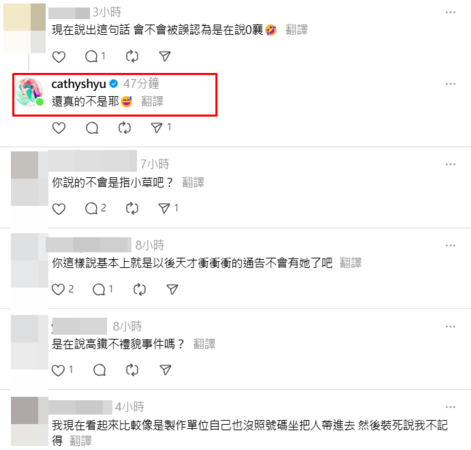
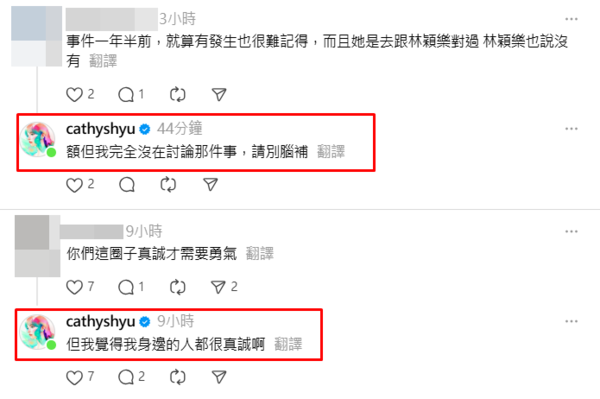
徐凱希解釋是她遇到了瞎人瞎事,「自身經驗太生氣想分享,請不要做連結。」她也在Instagram限時動態表示,發文當下完全沒聯想到新聞事件,「我只覺得自己很衰,想用文字抒發情緒而已,請各位饒過我吧。」

標題:徐凱希突開炮「說謊被拆穿還不認」!被疑影射林襄 急上火線:饒過我
聲明: 本文版權屬原作者。轉載內容僅供資訊傳遞,不涉及任何投資建議。如有侵權,請立即告知,我們將儘速處理。感謝您的理解。